Пусть прямая проходит через точку M1 (x1, y1, z1) и параллельна вектору (m ,n, l). Составим уравнение этой прямой.
Возьмем произвольную точку M (x, y, z) на этой прямой и найдем зависимость между x, y, z. Построим вектор 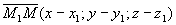
Векторы 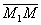 и
и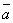 коллинеарны.
коллинеарны.
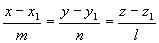 — каноническое уравнение прямой в пространстве.
— каноническое уравнение прямой в пространстве.
44 Параметрические уравнения прямой
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
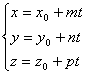
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
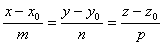
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора 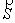 , которые могут быть вычислены по формулам:
, которые могут быть вычислены по формулам:
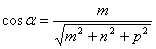
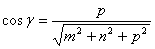
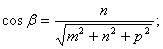
Отсюда получим: m : n : p = cosa : cosb : cosg.
Числа m, n, p называются угловыми коэффициентами прямой. Т.к.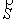 — ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
— ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
45 Уравнение прямой в пространстве, проходящее через две различные данные точки.
Уравнение прямой, проходящей через две данные точки.
Пусть на плоскости даны М1(х1у1) и М2(х2у2). Составим каноническое уравнение прямой, проходящей через эти две точки в качестве направляющего вектора S возьмем M1M2
тройка.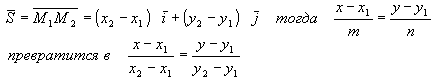
— это уравнение прямой, проходящей через две данные точки (х1 у1) и (х2, у2)
Перейдем теперь к уравнениям прямой и плоскости в пространстве.
Аналитическая геометрия в 3-мерном пространстве
Аналогично двумерному случаю любое уравнение первой степени относительно трех переменных x, y, z есть уравнение плоскости в пространстве Оxyz.. Общее уравнение плоскости АX + ВY + СZ + D = 0, где вектор N=(A,B,C) есть нормаль к плоскости. Каноническое уравнение плоскости, проходящей через точку М(х0,у0,z0) и имеющей нормаль N(А,В,С) А(х – х0) + В(у – у0) + С(z – z0)=0 – что представляет собой это уравнение?
Значения х –х0, у-у0 и z –z0 — это разности координат текущей точки и фиксированной точки. Следовательно, вектор а (х-х 0, у-у0, z-z0) -это вектор, лежащий в описываемой плоскости, а вектор N — вектор, перпендикулярный к плоскости, а значит, они перпендикулярны между собой.
Тогда их скалярное произведение должно равняться нулю.
В координатной форме (N,a)=0 выглядит так:
В пространстве различают правые и левые тройки векторов. Тройка некомпланарных векторов а, b, с называется правой, если наблюдателю из их общего начала обход концов векторов a, b, с в указанном порядке кажется совершающимся по часовой стрелке. В противном случае a,b,c — левая .
46 Угол между прямыми в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые: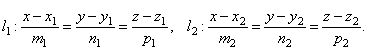
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами 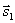 и
и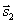 . Так как
. Так как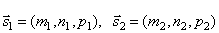 , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим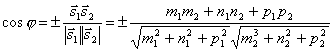
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 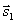 и
и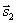 :
:
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда 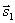 параллелен
параллелен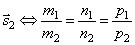 .
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .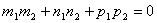
Найти уравнения прямой проходящей через точку М1(1;2;3) параллельно прямой l1:
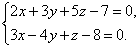
Поскольку искомая прямая l параллельна l1, то в качестве направляющего вектора искомой прямой l можно взять направляющий вектор прямой l1.

Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |

Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x y = m t + y
где N( x , y ) — координаты точки лежащей на прямой, a = < l , m >- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x , y ) лежащей на прямой и направляющего вектора a =
| x — x | = | y — y |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 |
x = l t + x |
| y = m t + y | |
| z = n t + z |
где ( x , y , z ) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x , y , z ) лежащей на прямой и направляющего вектора n =
| x — x | = | y — y | = | z — z |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.
Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.
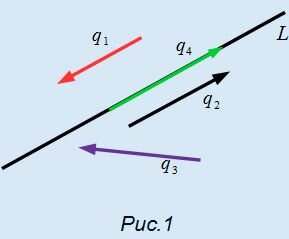 |
На рисунке Рис.1 представлена прямая L и векторы q1, q2, q3, q4. Из определения следует, что векторы q1, q2, q4 являются направляющими векторами прямой L, а q3 − нет.
Каноническое уравнение прямой L на плоскости представляется следующей формулой:
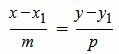 |
(1) |
где x1, y1 координаты некоторой точки M1 на прямой L. Вектор q=<m, p> является направляющим вектором прямой L.
Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к. направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя. В этом можно убедится, записав уравнение (1) в следующем виде:
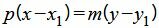 . . |
(2) |
Выше мы отметили, что прямая L проходит через точку M1(x1, y1). В этом можно убедится, подставив x=x1, y=y1 в уравнение (1).
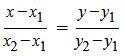 . . |
(3) |
Чтобы убедится, что точки M1(x1, y1) и M2(x2, y2) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M1 и M2. Получим тождества, следовательно эти точки принадлежат прямой L.
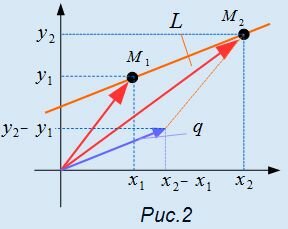 |
Сравним уравнения (1) и (3). Тогда можно записать q=<m, p>=<x2−x1, y2−y1>. На рисунке Рис.2 представлен вектор q, которая является разностью векторов, соответствующих точкам M2 и M1. Этот вектор является направляющим вектором прямой L. Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.
Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.
Онлайн калькулятор, для построения прямой через две точки находится тут.
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
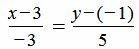 . . |
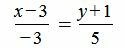 . . |
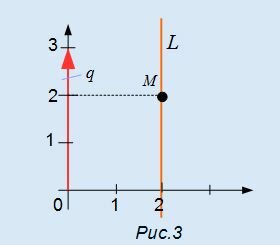
Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q=<0, 3>. Построить каноническое уравнение прямой.
Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
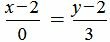 . . |
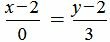 . . |
На рисунке Рис.3 изображена прямая L, точка M=(2, 2) и направляющий вектор q=<0, 3>. Прямая проходит через точку M и параллельна направляющему вектору q.
 |
Пример 3. Прямая проходит через точки M1=(−7, 2) и M2=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):
 . . |
Упростим полученное уравнение:
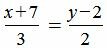 . . |
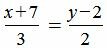 . . |
Приведение канонического уравнения прямой на плоскости к параметрическому виду
Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:
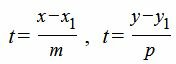 . . |
Выразим переменные x и y через t:
 , , |
(4) |
где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.
Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.
Обратное преобразование смотрите здесь.
Пример 4. Каноническое уравнение прямой задана следующим уравнением:
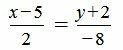 . . |
(5) |
Найти параметрическое уравнение прямой.
Решение. Обозначим через t левую и правую части уравнения (5):
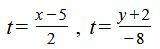 . . |
Выразим переменные x и y через t:
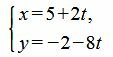 . . |
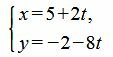 . . |
Приведение канонического уравнения прямой на плоскости к общему виду
Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:
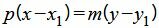 , , |
 . . |
(6) |
Сделаем следующие обозначения:
| A=p, B=−m, C=−px1+my1. |
Тогда уравнение (6) можно записать в следующем виде:
| Ax+By+C=0, |
где n=<A,B> − называется нормальным вектором прямой.
Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:
| (n,q)=(<A,B>,<m,p>) =(<p,−m>,<m,p>)=pm−mp=0. |
Обратное преобразование смотрите здесь.
Пример 5. Каноническое уравнение прямой задана следующим уравнением:
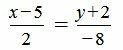 . . |
(7) |
Записать общее уравнение прямой.
Решение. Сделаем преобразования уравнения (7):

